Watershed

Include <mln/morpho/watershed.hpp>

template<class Label_t, class I, class N>
image_ch_value_t<I, Label_t> watershed(const Image<I> &ima, const Neighborhood<N> &nbh, int &nlabel, bool waterline = true)

Watershed by immersion as defined in [BM92]. The catchment basins are labeled from 1 to n, and the special label 0 is used for watershed lines.

Template Parameters:

Label_t – The type of label (must be signed Integral)

Parameters:

• input – Input image

• nbh – Neighborhood considered

• nlabel (out) – Number of catchment basins

• waterline – Add the watershed lines in the resulting segmentation

Returns:

A labelized image

Exception:

N/A

template<class Label_t, class I, class N, class S>
image_ch_value_t<I, Label_t> watershed_from_markers(I &&input, N &&nbh, S &&seeds, int &nlabel)

Watershed by immersion as defined in [BM92] with given markers. A marker is one pixel on the seed image which is greater than 0.

Template Parameters:

Label_t – The type of label (must be signed Integral) and the maximum value of this type must be higher or equal to the maximum value of the markers image value type.

Parameters:

• input – Input image

• nbh – The considered neighborhood

• seeds – An image with markers. The markers label should be greater than 0.

• nlabel (out) – The number of catchment basins

Returns:

A labelized image

Notes

Complexity

The algorithm is quasi-linear and requires \(n\) extra-memory space.

References

[BM92] (1,2)

Beucher, S., & Meyer, F. (1992). The morphological approach to segmentation: the watershed transformation. Optical Engineering-New York-Marcel Dekker Incorporated-, 34, 433-433.

Example 1: Cell segmentation

1. The distance transform is performed. Maxima correspond to cell centers. A dilation by a small disc removes the non-meaningfull maxima.

2. Invertion of the distance image so that maxima become minima

3. Watershed segmentation

4. Input labelization w.r.t in segmentation labels

  // (1) Compute the distance transform
  mln::se::wmask2d weights = {{3, 2, 3}, //
                                            {2, 0, 2},
                                            {3, 2, 3}};

  auto d = mln::labeling::chamfer_distance_transform<uint8_t>(input, weights);

  // Remove non-meaninfull extrema
  d = mln::morpho::dilation(d, mln::se::disc(5));

  // (2) Inverse the distance
  auto dinv = mln::transform(d, [](uint8_t x) -> uint8_t { return UINT8_MAX - x; });

  // (3) Run the watershed segmentation
  int  nlabel;
  auto ws = mln::morpho::watershed<int16_t>(dinv, mln::c8, nlabel);

  // (4) Labelize input
  auto output = mln::view::ifelse(ws == 0, 1, mln::view::ifelse(input, ws, 0));

Input image (note that blobs may touch)	Distance transform and dilation (after heat LUT)

Segmented blobs and watershed lines (labels displayed in false colors).

Example 2: Watershed from markers

This example demonstrates how to use the watershed based on input markers.

// (1) Get input image and markers image
mln::image2d<std::uint8_t> input = ...;
mln::image2d<std::uint16_t> seeds = ...;

// (2) Compute the Beucher gradient
auto grad = mln::morpho::gradient(input, mln::se::disc(3));

// (3) Compute the watershed
 auto out = mln::morpho::watershed_from_markers<std::int32_t>(grad, mln::c8, seeds, nlbl);

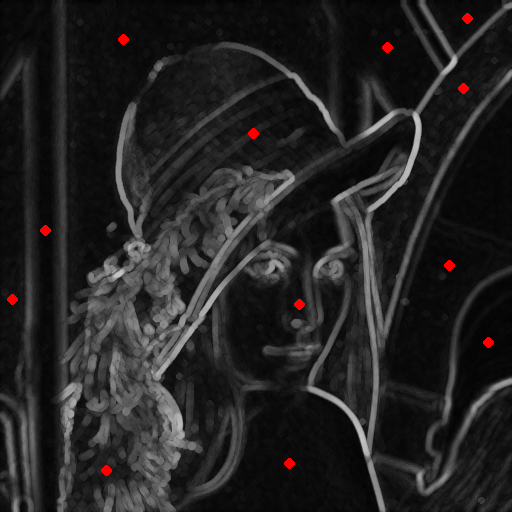
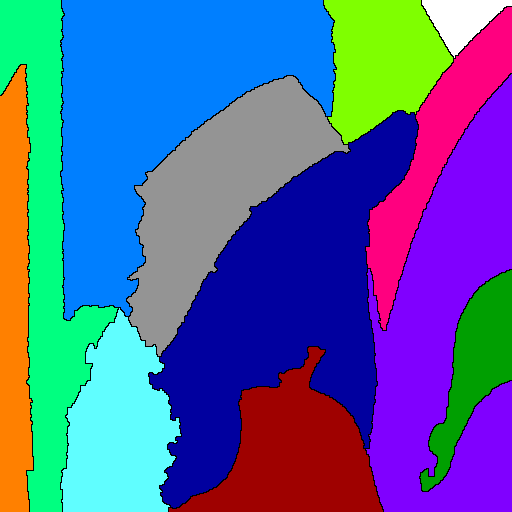
Input image (with markers in red)	Segmented image with watershed lines (labels are displayed in false colors).