Disc

class disc : public mln::se_facade<disc>

Create a disc of a given radius r with or without approximation.

The extent of the structuring will be 2*⌊r⌋+1. If an n-approximation is given, the radial decomposition of the disc is used when possible. The approximiation is a 2-n side polygon. If 0, the exact euclidean disc is used, that are all points \( \{p \mid |p| \le r\} \)

Property
Incremental	Yes if created with no-approximation
Decomposable	Yes if created with approximation
Separable	No

Public Types

enum approx

Enumeration of disc approximation.

Values:

enumerator EXACT

No approximation.

enumerator PERIODIC_LINES_8

Approximation with 8 periodic lines.

Public Functions

explicit disc(float radius, approx approximation = PERIODIC_LINES_8)

Constructs a disc of radius r with a given approximation.

Parameters:

• radius – The radius r of the disc.

• approximation – The disc approximation

inc_type inc() const

A WNeighborhood to be added when used incrementally.

Throws:

std::runtime_error – if the disc is not incremental

inc_type dec() const

A WNeighborhood to be substracted when used incrementally.

Throws:

std::runtime_error – if this disc is not incremental

std::vector<mln::se::periodic_line2d> decompose() const

Return a range of SE for decomposition.

Throws:

std::runtime_error – if not decomposable

::ranges::span<point2d> offsets() const

Return a range of SE offsets.

::ranges::span<point2d> before_offsets() const

Return a range of SE offsets before center.

::ranges::span<point2d> after_offsets() const

Return a range of SE offsets after center.

bool is_decomposable() const

True if the SE is decomposable (i.e. constructed with approximation)

bool is_incremental() const

True if the SE is incremental (i.e. constructed with no-approximation)

inline float radius() const

Returns the radius of the disc.

inline int radial_extent() const

Returns the extent radius.

mln::box2d compute_input_region(mln::box2d roi) const

Return the input ROI for 2D box.

mln::box2d compute_output_region(mln::box2d roi) const

Return the output ROI for 2D box.

Approximated discs

Quality of the approximation

The approximated disc 𝔇ₐ of the true euclidean disc 𝔇 uses a radial decomposition in 8 periodic lines \(k_i.L_\theta\) of orientations θ ∈ {0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°} and length kᵢ.

Such approximation introduces an error:

\[err = \frac{|\mathcal{D} \Delta \mathcal{D}_a|}{r}\]

Below is the error of our approximation, the 8-approximation of matlab and the best approximation possible using 8 periodic lines (computed by exhaustive search).

Euclidean disc	Matlab 8-appoximated disc	Our appoximated disc

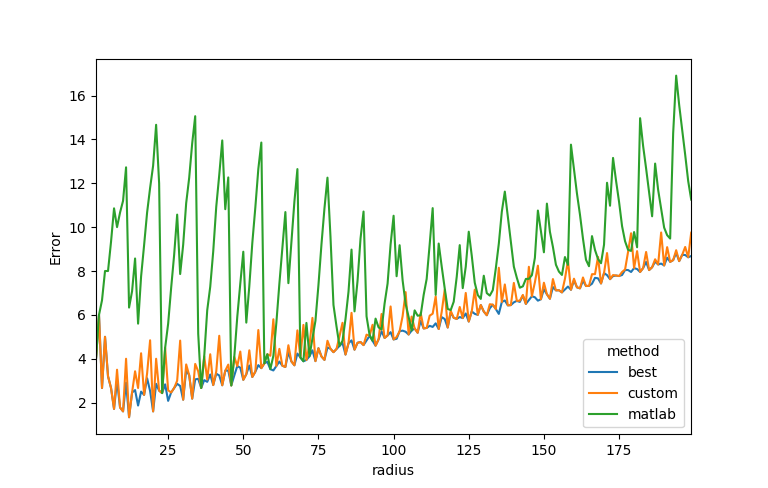
Error of our disc approximation (labeled custom above), matlab approximation and the best appromximation relative to the euclidean disc.

Performance

Using approximated disc can speed up the running of some morphological operations. Below is the running time of the dilation by the euclidean disc vs the approximated disc.

(Source code)

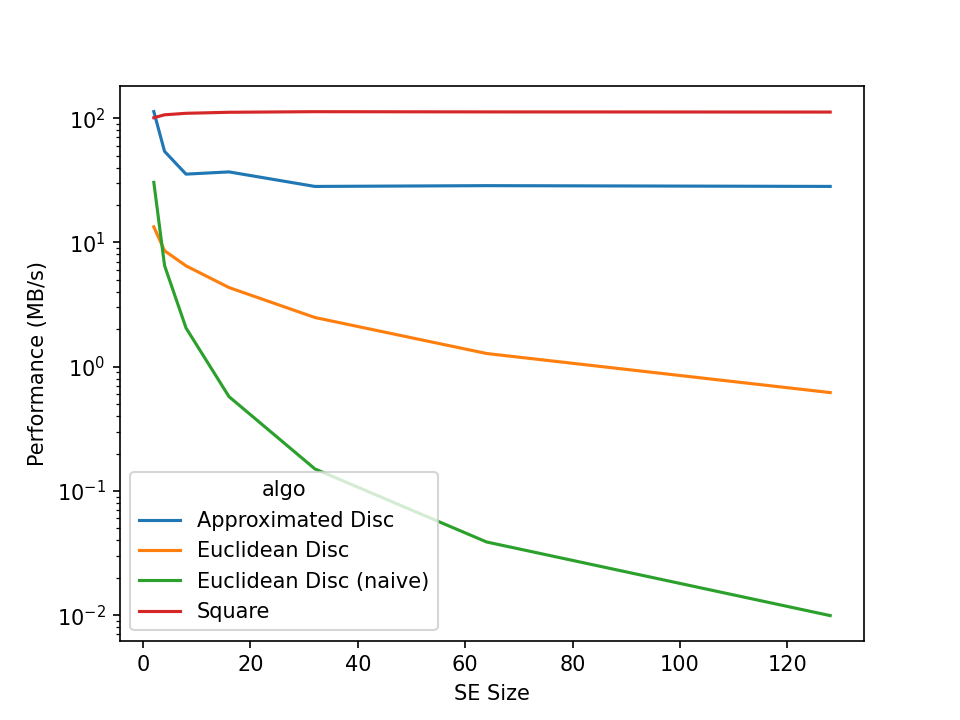
Dilation by a square is given as reference. The running time of the dilation by the approximated disc does not depend on the radius (like for a square) because it uses a decomposition in periodic lines (the SE is decomposable) [Adam93] [JoSo96a] [JoSo96b]. The dilation by the euclidean disc is \(O(r.n)\) because of the optimization of incremental SEs by [VaTa96]. It contrasts with the naive implementation which is \(O(r^2.n)\) for disc.

References

[Adam93]

Adams, R. (1993), ‘Radial decomposition of discs and spheres.’, Computer Vision, Graphics, and Image Processing: Graphical Models and Image Processing 55(5), 325–332.

[JoSo96a]

Jones, R., & Soille, P. (1996). Periodic lines: Definition, cascades, and application to granulometries. Pattern Recognition Letters, 17(10), 1057-1063.

[JoSo96b]

Jones, R., & Soille, P. (1996). Periodic lines and their application to granulometries. In Mathematical Morphology and its Applications to Image and Signal Processing (pp. 263-272). Springer, Boston, MA.

[VaTa96]

Van Droogenbroeck, M., & Talbot, H. (1996). Fast computation of morphological operations with arbitrary structuring elements. Pattern recognition letters, 17(14), 1451-1460.